Spin torques due to the flow of spin-polarised currents through a ferromagnetic material can lead to novel phenomena that are inaccessible with magnetic fields alone. An emblematic example are self-sustained magnetisation oscillations driven by d.c. currents, which arise when the spin-torques compensate on average the magnetic dissipation in the system. When such effects arise in magnetoresistive multilayers, such as spin valves or magnetic tunnel junctions, the oscillations result in periodic variations in the multilayer resistance. This is the basis of spin-torque nano-oscillators (STNO). Because of their compact size and strong frequency nonlinearity, such devices have been touted for possible applications as tuneable radiofrequency electrical oscillators, field sensors, and building blocks for neuro-inspired applications such as associative memories.
Besides output power, a key performance metric is the spectral linewidth of the oscillator, as this is characteristic of the coherence time of the underlying oscillations. Along with collaborators at Oakland University (Michigan, USA), the NOMADE group developed the pioneering stochastic theories to describe the power spectrum of STNOs. We showed that the frequency nonlinearity results in a strong coupling between the phase and amplitude fluctuations, which can result in an inhomogeneous broadening of the power spectrum. Moreover, a more sophisticated analysis based on the Fokker-Planck equation allowed us to predict an asymmetric broadening of the spectral line near the current threshold for self-oscillation, which was subsequently confirmed in experiments in the NOMADE group.
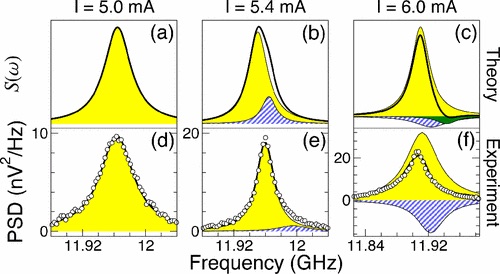
Using time-resolved electrical measurements, the NOMADE group also provided the first experimental evidence of phase-amplitude coupling in an STNO based on magnetic tunnel junctions. These measurements also allow the frequency nonlinearity parameter to be extracted directly.
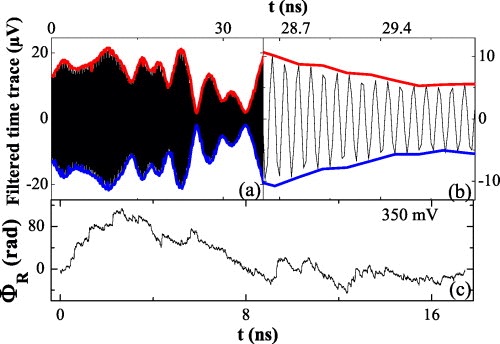
This body of work underpins many applications of STNO today and is widely used in the analysis of experimental data in academia and industry.
Further reading:
- J.-V. Kim, Phys. Rev. B 73, 174412 (2006).
- J.-V. Kim, V. S. Tiberkevich & A. N. Slavin, Phys. Rev. Lett. 100, 017207 (2008).
- J.-V. Kim, Q. Mistral, C. Chappert, V. S. Tiberkevich & A. N. Slavin, Phys. Rev. Lett. 100, 167201 (2008).
- L. Bianchini, S. Cornelissen, J.-V. Kim, T. Devolder, W. Van Roy, L. Lagae & C. Chappert, Appl. Phys. Lett. 97, 032502 (2010).
- J.-V. Kim, Spin torque oscillators, in vol. 63 of Solid State Physics, R. E. Stamps and R. E. Camley, eds. (Academic Press, 2012).
